AM–FM Components
A component triplet Tuple{Function,Function,Real} maps to an AM–FM component AMFMcomp.
This mapping is provided in the ISA module.
using ISADefining an AM–FM Component
We define an AM–FM component AMFMcomp by passing the function AMFMcomp() a cannonical triplet. First define a cannonical triplet.
a₀(t) = exp(-t^2)
ω₀(t) = 2.0
φ₀ = 0.0
𝐶₀ = (a₀,ω₀,φ₀)Then pass the cannonical triplet to the function AMFMcomp().
julia> ψ₀ = AMFMcomp(𝐶₀)
AMFMcomp(a₀, ω₀, 0.0)We also allow an AM–FM component AMFMcomp to be defined by passing the function AMFMcomp() an instantaneous amplitude (IA) Function, an instantaneous frequency (IF) Function, and a phase reference Real.
a₀(t) = exp(-t^2)
ω₀(t) = 2.0
φ₀ = 0.0Then calling the function AMFMcomp() as follows.
julia> ψ₀ = AMFMcomp(a₀,ω₀,φ₀)
AMFMcomp(a₀, ω₀, 0.0)Evaluating an AM–FM Component
Once an AM–FM component AMFMcomp is defined it can be evaluated at a time instant Float64
julia> t₀ = 0.15
julia> ψ₀(t₀)
-0.302141748563871 + 0.9298966854483709imor over a range of time instants Array{Float64,1}.
julia> t = 0.0:0.25:1.0
julia> ψ₀(t)
5-element Array{Complex{Float64},1}:
1.0 + 0.0im
-0.9394130628134758 + 1.1504492004517347e-16im
0.7788007830714049 - 1.9075117723236962e-16im
-0.569782824730923 + 2.0933481375475864e-16im
0.36787944117144233 - 1.8020895204108955e-16imAnother example of evaluating an AM–FM component over a range of time instants using the Plots module follows.
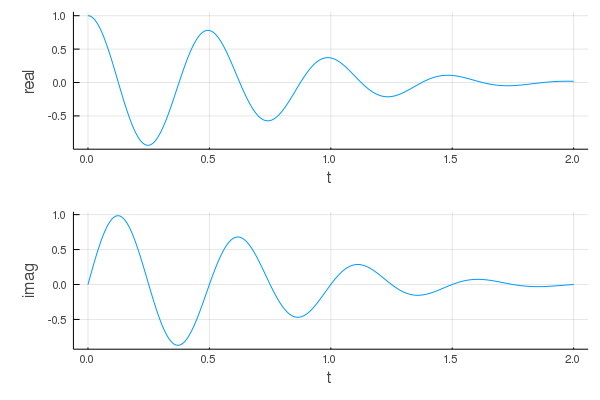
using Plots
t = 0.0:0.005:2.0
p1 = plot(t, real(ψ₀(t)), xlab="t", ylab="real", legend = :false)
p2 = plot(t, imag(ψ₀(t)), xlab="t", ylab="imag", legend = :false)
plot(p1, p2, layout = (2,1))